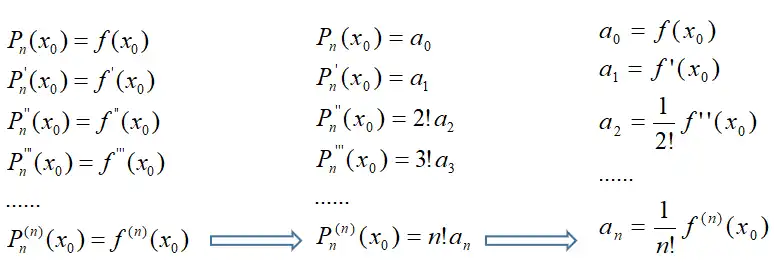中值定理

我们可以这样写：

f(x)=f(x0)+f′(x0)(x−x0)+o(x−x0)f(x)=f\left(x_0\right)+f^{\prime}\left(x_0\right)\left(x-x_0\right)+o\left(x-x_0\right)

因为 f′(x0)=lim⁡x→x0f(x)−f(x0)x−x0f^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}，所以上式成立。而 o(x−x0)o\left(x-x_0\right) 是无穷小量，所以 f(x)≈f(x0)+f′(x0)(x−x0)f(x) \approx f\left(x_0\right)+f^{\prime}\left(x_0\right)\left(x-x_0\right)。

从几何上看，它是用切线近似代替曲线。然而，这样的近似是比较粗糙的，而且只在点的附近才有近似意义。为了改善上述不足，使得近似替代更加精密，数学家们在柯西中值定理的基础上，推导出了泰勒中值定理（泰勒公式）。

推导过程

给定一个函数 f(x)f(x)，要找一个在指定点 x0x_0 附近与 f(x)f(x) 很近似的多项式函数 P(x)P(x)，记为：

Pn(x)=a0+a1(x−x0)+a2(x−x0)2+⋯+an(x−x0)nP_n(x)=a_0+a_1\left(x-x_0\right)+a_2\left(x-x_0\right)^2+\cdots+a_n\left(x-x_0\right)^n

使得 f(x)≈Pn(x)f(x) \approx P_n(x) 可估计。那么，该多项式要满足什么条件，误差又是什么？

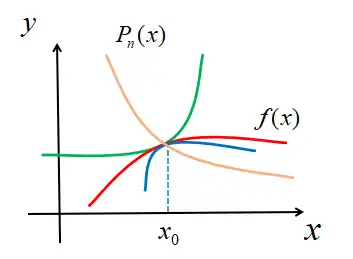
从几何上看，y=f(x),y=Pn(x)y=f(x), y=P_n(x) 代表两条曲线，如下图：

使它们在 x0x_0 附近很靠近，很明显：

  1. 首先要求两曲线在点 (x0,f(x0))\left(x_0, f\left(x_0\right)\right) 相交，即 Pn(x0)=f(x0)P_n\left(x_0\right)=f\left(x_0\right)；
  2. 如果要靠得更近，还要求两曲线在点 (x0,f(x0))\left(x_0, f\left(x_0\right)\right) 相切（由图像可以直观看出，相交：橙色 和 红色 图像；相切：绿色 和 红色 图像，两曲线在 x0x_0 附近的靠近情况明显差异很大，相切更近），即 Pn′(x0)=f′(x0)P_n^{\prime}\left(x_0\right)=f^{\prime}\left(x_0\right)；
  3. 如果还要靠得更近，还要求曲线在点 (x0,f(x0))\left(x_0, f\left(x_0\right)\right) 弯曲方向相同（如上图，弯曲方向相反：绿色 和 红色 图像；弯曲方向相同：蓝色 和 红色 图像，明显在离 x0x_0 很远的地方，弯曲方向相同两函数的差异更小一点），即 Pn′′(x0)=f′′(x0)P_n^{\prime \prime}\left(x_0\right)=f^{\prime \prime}\left(x_0\right)，进而可猜想，若在 (x0,f(x0))\left(x_0, f\left(x_0\right)\right) 附近有 Pn′(x0)=f′(x0)P_n^{\prime}\left(x_0\right)=f^{\prime}\left(x_0\right)，Pn′′(x0)=f′′(x0)P_n^{\prime \prime}\left(x_0\right)=f^{\prime \prime}\left(x_0\right)，……，Pn(n)(x0)=f(n)(x0)P_{n}^{(n)}\left(x_{0}\right)=f^{(n)}\left(x_{0}\right)，近似程度越来越好。

综上所述，所要找的多项式应满足下列条件：

如何得出结论的呢？以上图三行二阶导数为例：

  1. 第一个箭头：将 Pn(x)P_{n}(x) 求二阶导后代入 x0x_0，求得 Pn′′(x0)=2!a2P_{n}^{\prime \prime}\left(x_{0}\right)=2 ! a_{2}。
  2. 第二个箭头：所以 f′′(x0)=2!a2f^{\prime \prime}\left(x_{0}\right)=2 ! a_{2}，所以 a2=12!f′′(x0)a_{2}=\frac{1}{2 !} f^{\prime \prime}\left(x_{0}\right)，多项式函数：

Pn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)nP_{n}(x)=a_{0}+a_{1}\left(x-x_{0}\right)+a_{2}\left(x-x_{0}\right)^{2}+\ldots+a_{n}\left(x-x_{0}\right)^{n}

其中系数 aa 可全用 f(x)f(x) 表示，得：

Pn(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)nP_{n}(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\ldots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}

其中误差 Rn(x)=f(x)−Pn(x)R_{n}(x)=f(x)-P_{n}(x)。因为是用多项式函数去无限逼近给定的函数，所以两者之间肯定存在一些误差。

这样，我们就得到了泰勒公式的定义：

如果函数 f(x)f(x) 在含 x0x_0 的某个开区间 (a,b)(a, b) 内具有直到 (n+1)(n+1) 阶导数，则对 ∀x∈(a,b)\forall x \in(a, b)，有:

f(x)=f(x0)0!+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+Rn(x)f(x)=\frac{f\left(x_{0}\right)}{0 !}+\frac{f^{\prime}\left(x_{0}\right)}{1 !}\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\ldots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+R_{n}(x)

其中余项（即误差）：

Rn(x)=f(n+1)(ξ)(n+1)!(x−x0)n+1R_{n}(x)=\frac{f^{(n+1)}(\xi)}{(n+1) !}\left(x-x_{0}\right)^{n+1}

ξ\xi 在 x0x_0 与 xx 之间。这种余项表达方式称为 nn 阶泰勒展开式的拉格朗日余项。拉格朗日余项是 nn 阶泰勒公式又多展开了一阶，nn 变为 n+1n+1。

麦克劳林公式

这是泰勒公式的一种特殊情况：即当 x0=0x_0=0 时的泰勒公式。所以将 x0=0x_0=0 带入公式，即得：

f(x)=f(0)0!+f′(0)1!x+f′′(0)2!x2+…+f(n)(0)n!xn+Rn(x)f(x)=\frac{f(0)}{0 !}+\frac{f^{\prime}(0)}{1 !} x+\frac{f^{\prime \prime}(0)}{2 !} x^{2}+\ldots+\frac{f^{(n)}(0)}{n !} x^{n}+R_{n}(x)

几个常见的初等函数的带有佩亚诺余项的麦克劳林公式：

  • ex=1+x+12!x2+…+1n!xn+o(xn)e^{x}=1+x+\frac{1}{2 !} x^{2}+\ldots+\frac{1}{n !} x^{n}+o\left(x^{n}\right)
  • sin⁡x=x−13!x3+…+(−1)m−1(2m−1)!x2m−1+o(x2m−1)\sin x=x-\frac{1}{3 !} x^{3}+\ldots+\frac{(-1)^{m-1}}{(2 m-1) !} x^{2 m-1}+o\left(x^{2 m-1}\right)
  • cos⁡x=1−12!x2+14!x4−…+(−1)m(2m)!x2m+o(x2m)\cos x=1-\frac{1}{2 !} x^{2}+\frac{1}{4 !} x^{4}-\ldots+\frac{(-1)^{m}}{(2 m) !} x^{2 m}+o\left(x^{2 m}\right)
  • ln⁡(1+x)=x−12x2+13x3−…+(−1)n−1nxn+o(xn)\ln (1+x)=x-\frac{1}{2} x^{2}+\frac{1}{3} x^{3}-\ldots+\frac{(-1)^{n-1}}{n} x^{n}+o\left(x^{n}\right)

佩亚诺余项为 (x−x0)n\left(x-x_{0}\right)^{n} 的高阶无穷小：Rn(x)=o[(x−x0)n]R_{n}(x)=o\left[\left(x-x_{0}\right)^{n}\right]。